Motor Trend Car Road Tests (mtcars) datasets - Analysis and Regression
Motor Trend Car Road Tests (mtcars) datasets - Analysis and Regression
This assignment was part of the Johns Hopkins Coursera module on Regression Models as part of the Data Sciene Specialization.
Source code available on GitHub
Summary
We want to answer these two questions:
- Is an automatic or manual transmission better for MPG?
- Quantify the MPG difference between automatic and manual transmissions?
We compared the mean mpg for automatic and manual transmission and concluded the difference in favor of manual tranmission in terms of mpg was significant. We then looked further to check other variables to explain the difference in mpg.
Look at the data
Glimpse at the data.
## mpg cyl disp hp drat wt qsec vs am gear carb mean.mpg
## 1 21.0 6 160 110 3.90 2.620 16.46 v.shaped manual 4 4 20.09062
## 2 21.0 6 160 110 3.90 2.875 17.02 v.shaped manual 4 4 20.09062
## 3 22.8 4 108 93 3.85 2.320 18.61 straight manual 4 1 20.09062
## mpg cyl disp hp
## Min. :10.40 Min. :4.000 Min. : 71.1 Min. : 52.0
## 1st Qu.:15.43 1st Qu.:4.000 1st Qu.:120.8 1st Qu.: 96.5
## Median :19.20 Median :6.000 Median :196.3 Median :123.0
## Mean :20.09 Mean :6.188 Mean :230.7 Mean :146.7
## 3rd Qu.:22.80 3rd Qu.:8.000 3rd Qu.:326.0 3rd Qu.:180.0
## Max. :33.90 Max. :8.000 Max. :472.0 Max. :335.0
## drat wt qsec vs
## Min. :2.760 Min. :1.513 Min. :14.50 v.shaped:18
## 1st Qu.:3.080 1st Qu.:2.581 1st Qu.:16.89 straight:14
## Median :3.695 Median :3.325 Median :17.71
## Mean :3.597 Mean :3.217 Mean :17.85
## 3rd Qu.:3.920 3rd Qu.:3.610 3rd Qu.:18.90
## Max. :4.930 Max. :5.424 Max. :22.90
## am gear carb
## automatic:19 Min. :3.000 Min. :1.000
## manual :13 1st Qu.:3.000 1st Qu.:2.000
## Median :4.000 Median :2.000
## Mean :3.688 Mean :2.812
## 3rd Qu.:4.000 3rd Qu.:4.000
## Max. :5.000 Max. :8.000
MPG difference between automatic and manual transmission
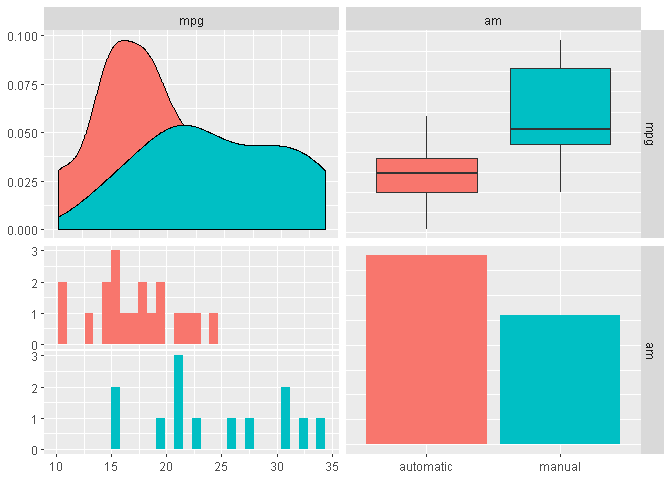
Looking at the boxplot we see a difference between the two transmission type’s mpg.
We check normality, variance equality to see how we can conduct our test (details in appendix), and then conducted a two-sided T-Test:
mpg.test <- t.test(auto, manual, alternative="two.sided", paired=FALSE, var.equal = FALSE)
We have a p-value of 0.14% < 5%, and a confidence interval [-11 ; -3.2] for the difference of mean mpg between automatic and manual excluding 0.
From the look of this manual transmission allows for more mpg with 0 more mpg in average.
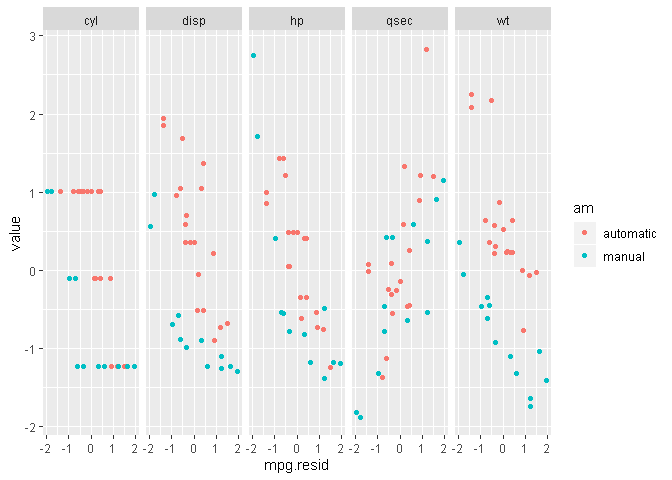
If we fit a simple linear model to our data we end up with similar results as previously (increased of roughly 7.2 mpg), and we can have a look at the residual plot, which are alost normal (graphically speaking) for automatic but not as much for manual. Looking at the reisudals against several other possible predictors, we can see some linear trends (e.g. hp and wt).
Going further
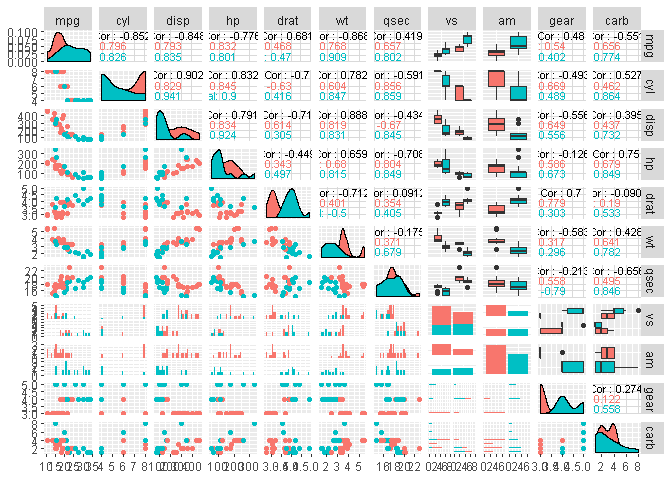
Looking at pairplot and correlation plot we see that other variables since more correlated with mpg than am.
ggpairs(mtcars, aes(colour = am), columns = seq(1,11,1),
progress=FALSE, upper = list(continuous = wrap("cor", size = 3)))
mtcars.cor <- cor(mtcars %>% mutate(am=as.numeric(am), vs=as.numeric(vs)) %>% select(-c(mean.mpg)))
corrplot(mtcars.cor, type = "upper", order = "hclust", tl.col = "black", tl.srt = 45)
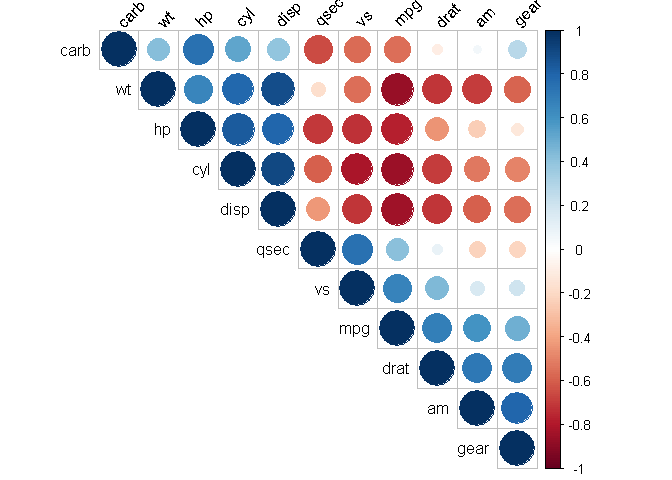
Adding variables to our model
We can try to add wt, cyl and disp wich seems to be relevant candidates both from mechanical point of view and from the corrplot.
rownames(mtcars) <- rownames(datasets::mtcars)
fit2<-lm(mpg~I(hp/10)+wt+cyl+disp+am,mtcars)
summary(fit2)
##
## Call:
## lm(formula = mpg ~ I(hp/10) + wt + cyl + disp + am, data = mtcars)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.5952 -1.5864 -0.7157 1.2821 5.5725
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 38.20280 3.66910 10.412 9.08e-11 ***
## I(hp/10) -0.27960 0.13922 -2.008 0.05510 .
## wt -3.30262 1.13364 -2.913 0.00726 **
## cyl -1.10638 0.67636 -1.636 0.11393
## disp 0.01226 0.01171 1.047 0.30472
## ammanual 1.55649 1.44054 1.080 0.28984
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.505 on 26 degrees of freedom
## Multiple R-squared: 0.8551, Adjusted R-squared: 0.8273
## F-statistic: 30.7 on 5 and 26 DF, p-value: 4.029e-10
Only weight, hp and tranmission type seems significant.
Modelling withough transmission type
fit3<-lm(mpg~I(hp/10)+wt+cyl+disp,mtcars)
summary(fit3)
##
## Call:
## lm(formula = mpg ~ I(hp/10) + wt + cyl + disp, data = mtcars)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.0562 -1.4636 -0.4281 1.2854 5.8269
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 40.82854 2.75747 14.807 1.76e-14 ***
## I(hp/10) -0.20538 0.12147 -1.691 0.102379
## wt -3.85390 1.01547 -3.795 0.000759 ***
## cyl -1.29332 0.65588 -1.972 0.058947 .
## disp 0.01160 0.01173 0.989 0.331386
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.513 on 27 degrees of freedom
## Multiple R-squared: 0.8486, Adjusted R-squared: 0.8262
## F-statistic: 37.84 on 4 and 27 DF, p-value: 1.061e-10
anova(fit2,fit3)
## Analysis of Variance Table
##
## Model 1: mpg ~ I(hp/10) + wt + cyl + disp + am
## Model 2: mpg ~ I(hp/10) + wt + cyl + disp
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 26 163.12
## 2 27 170.44 -1 -7.3245 1.1675 0.2898
We see we have similar R-square, RSS and p-value while droping the transmission type.
Automatic model selection
Let’s try some automatic model selection to see what we could get.
library(MASS)
##
## Attaching package: 'MASS'
## The following object is masked from 'package:dplyr':
##
## select
# Fit the full model
full.model <- lm(mpg ~., data = datasets::mtcars)
# Stepwise regression model
step.model <- stepAIC(full.model, direction = "both",
trace = FALSE)
summary(step.model)
##
## Call:
## lm(formula = mpg ~ wt + qsec + am, data = datasets::mtcars)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.4811 -1.5555 -0.7257 1.4110 4.6610
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 9.6178 6.9596 1.382 0.177915
## wt -3.9165 0.7112 -5.507 6.95e-06 ***
## qsec 1.2259 0.2887 4.247 0.000216 ***
## am 2.9358 1.4109 2.081 0.046716 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.459 on 28 degrees of freedom
## Multiple R-squared: 0.8497, Adjusted R-squared: 0.8336
## F-statistic: 52.75 on 3 and 28 DF, p-value: 1.21e-11
We find again wt and am which confort us in our previous models. We also have an additional variable that we did not explore before: qsec.
We can however argue that qsec is strongly correlated with horsepower (and cylinder, displacement, etc.)
Some PCA
library("FactoMineR")
library("factoextra")
## Welcome! Related Books: `Practical Guide To Cluster Analysis in R` at https://goo.gl/13EFCZ
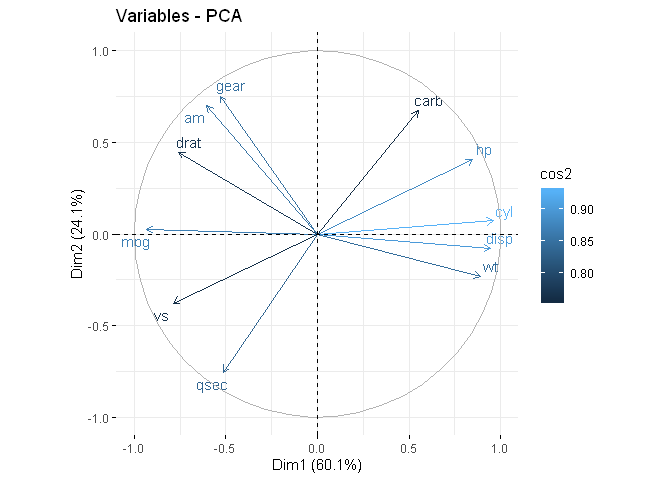
res.pca <- PCA(datasets::mtcars, scale.unit = TRUE, ncp = 5, graph = FALSE)
fviz_pca_var(res.pca, col.var = "cos2", repel = TRUE)
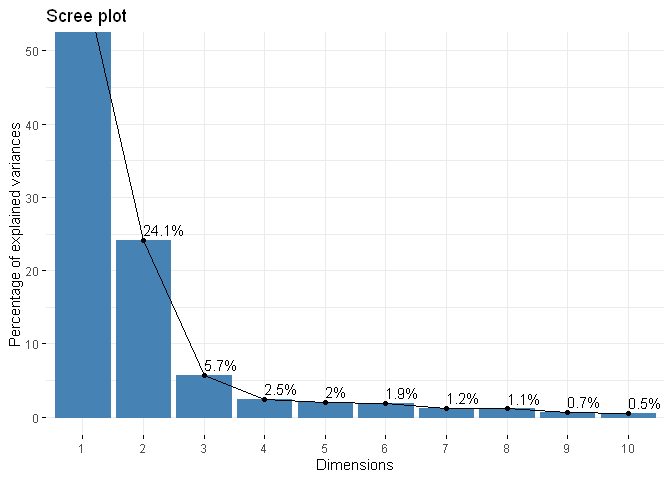
fviz_eig(res.pca, addlabels = TRUE, ylim = c(0, 50))
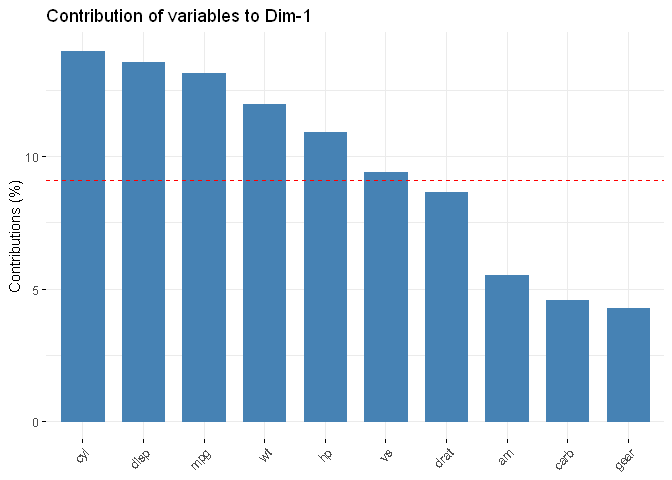
fviz_contrib(res.pca, choice = "var", axes = 1, top = 10)
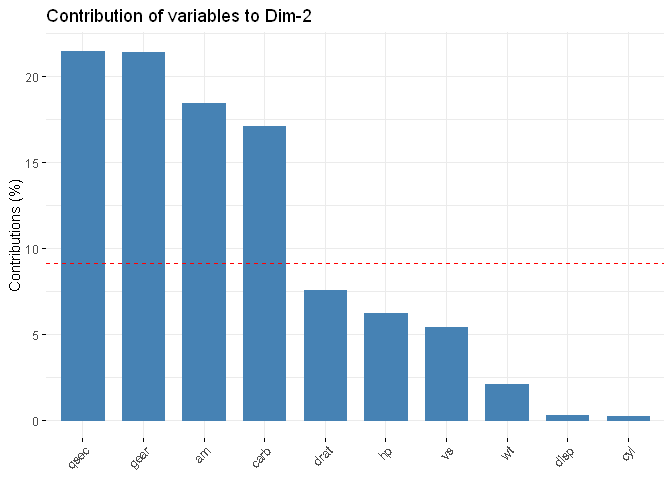
fviz_contrib(res.pca, choice = "var", axes = 2, top = 10)
Normality and variance
Normality of data
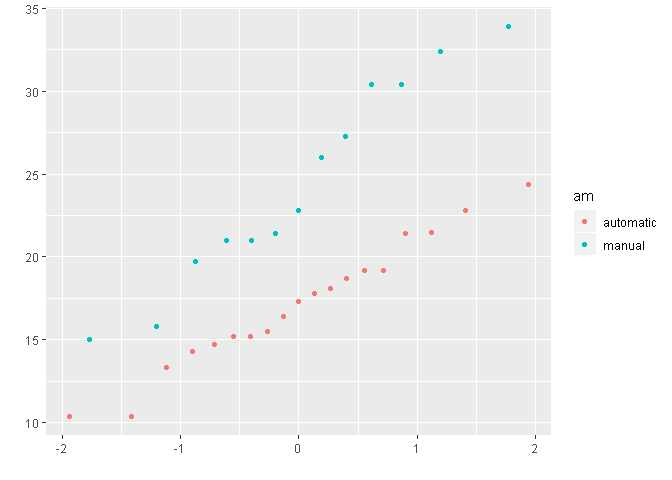
shapiro.test(manual)
##
## Shapiro-Wilk normality test
##
## data: manual
## W = 0.9458, p-value = 0.5363
shapiro.test(auto)
##
## Shapiro-Wilk normality test
##
## data: auto
## W = 0.97677, p-value = 0.8987
Comparison of variance
var.test(auto, manual)
##
## F test to compare two variances
##
## data: auto and manual
## F = 0.38656, num df = 18, denom df = 12, p-value = 0.06691
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
## 0.1243721 1.0703429
## sample estimates:
## ratio of variances
## 0.3865615
T-Test
mpg.test <- t.test(auto, manual, alternative="two.sided", paired=FALSE, var.equal = FALSE)
mpg.test
##
## Welch Two Sample t-test
##
## data: auto and manual
## t = -3.7671, df = 18.332, p-value = 0.001374
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -11.280194 -3.209684
## sample estimates:
## mean of x mean of y
## 17.14737 24.39231
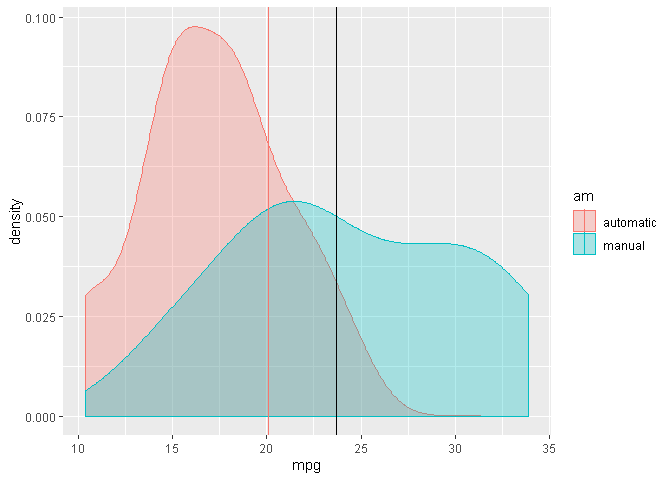
Residual plots
fit<-lm(mpg ~ am, mtcars)
qplot(residuals(fit), color=mtcars$am, geom = 'density')

mtcars$mpg.resid <- residuals(fit)
mtcars.gathered <- mtcars %>% dplyr::select(am, mpg.resid, cyl, disp, hp, wt, qsec) %>% mutate_if(is.numeric, scale) %>% gather(key, value, -c(am,mpg.resid))
ggplot(mtcars.gathered, aes(x = mpg.resid, y = value, color=am)) +
geom_point() +
facet_grid(. ~ key)